SakiiR blog

VolgaCTF 2020 DotNetMe

6 min read dotnet reverse

task.png

Introduction

DotNetMe is obviously a Windows reverse task.

Two binaries are provided:

  • A PE32+ executable file (console)
  • Another PE32+ DLL

Both binary are .NET binaries are expected and are heavily obfuscated.

Technical details

At first, we could see that both of the binaries are obfuscated and hard to read:

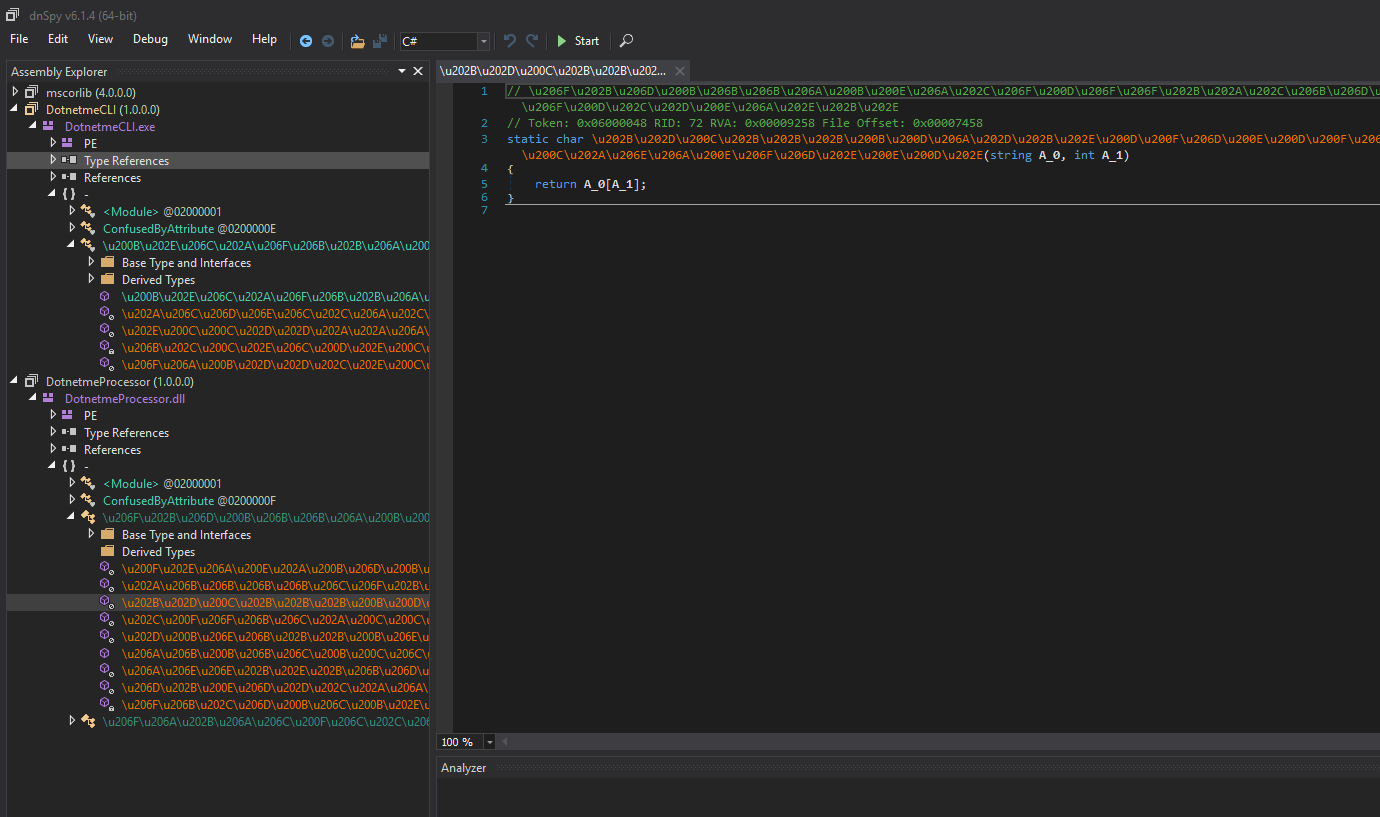
obfuscated.png

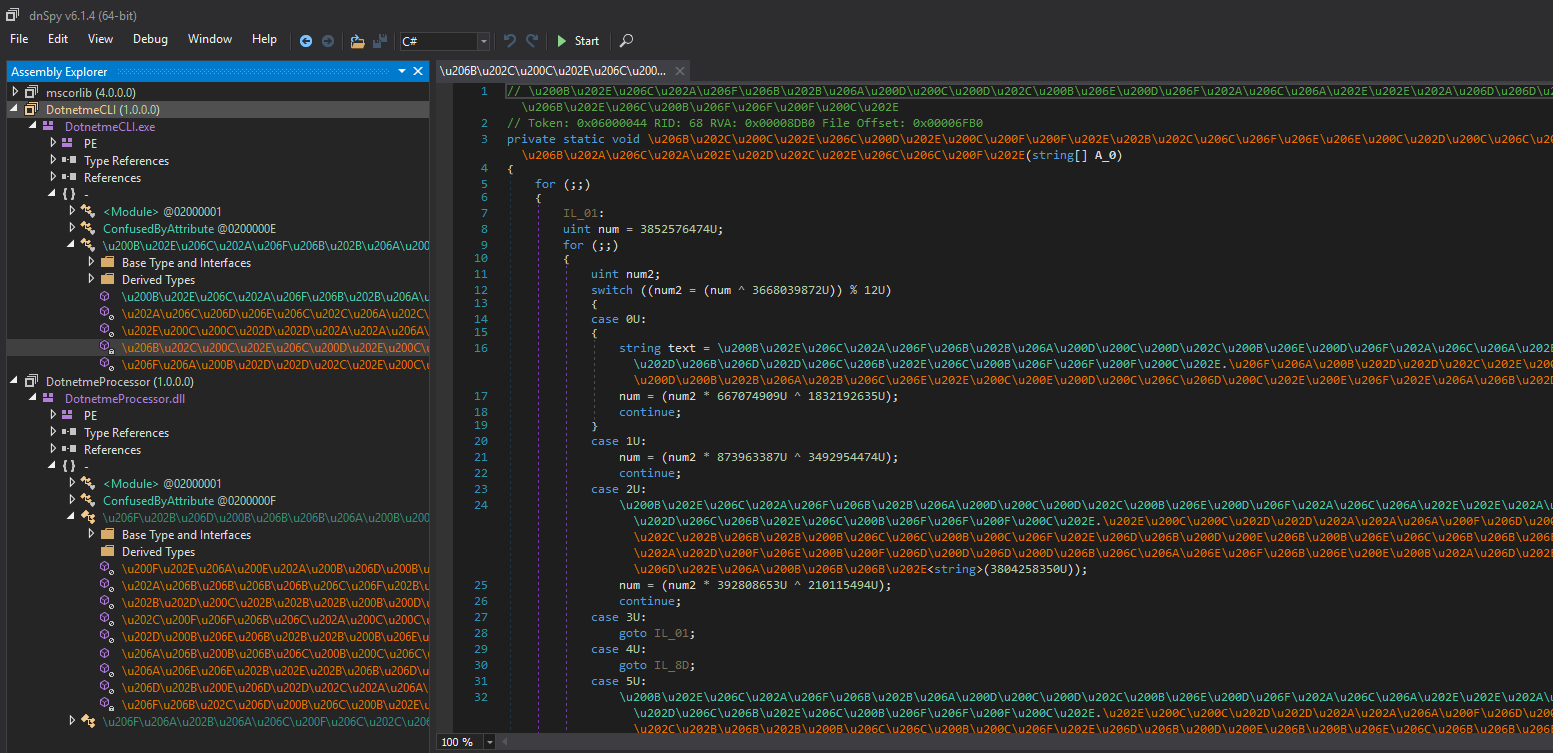
obfuscated2.png

In fact, the symbol names are displayed in some kind of Unicode and all the logic is behind a “state machine”. Each code scope is executed depending on the value of a global 32-bit integer.

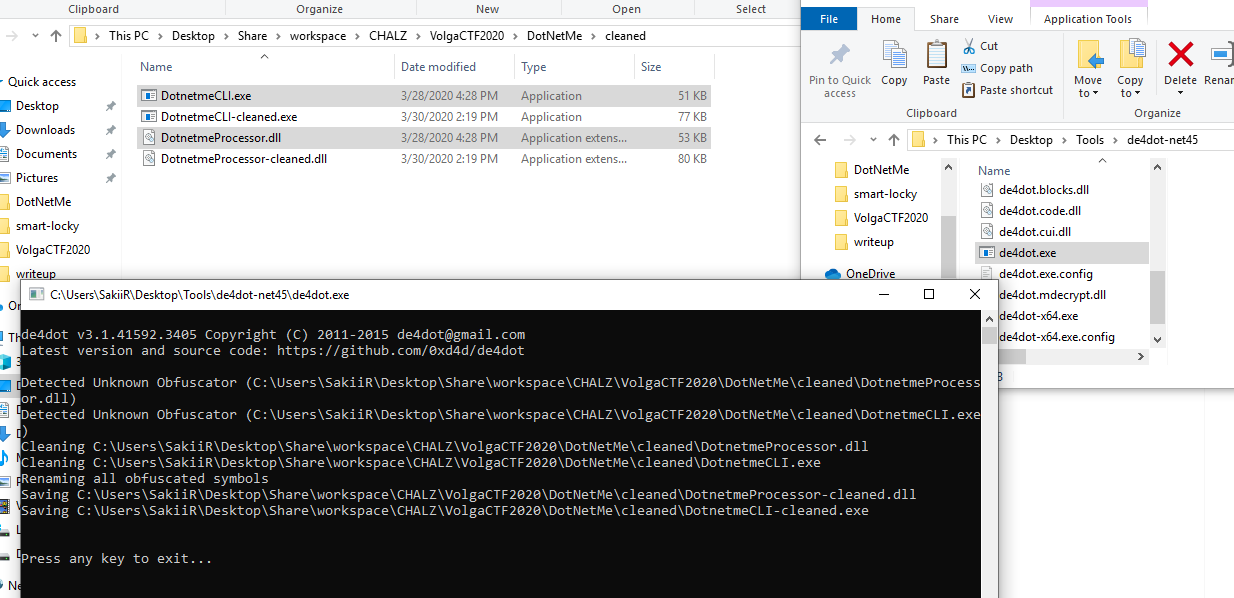
The first thing I did to avoid burning my eyes was to run de4dot (https://github.com/0xd4d/de4dot) against the two binary. This tool is helping us have simple method names like method_1, method_2, etc.

So we just drag and drop the two binaries on the de4dot.exe executable file and our two binaries get cleaned:

de4dot.png

Now, let’s import these into dnSpy (https://github.com/0xd4d/dnSpy OpenSource .NET debugger and assembly editor):

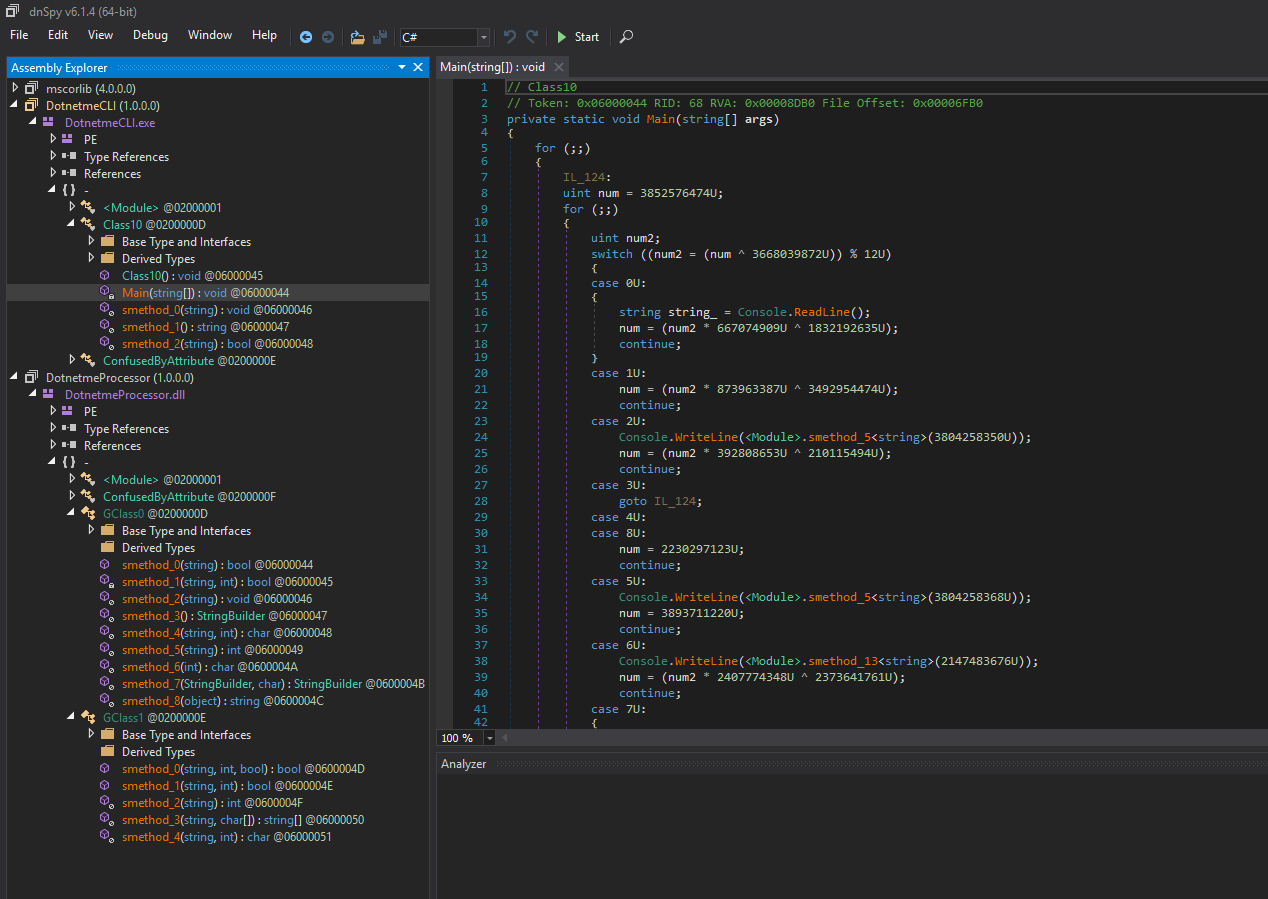
cleaned_with_de4dot.png

dnSpy is a cool tool that allows us to put breakpoint and see scoped local variables. Unfortunately, in this case, for some reason (Antidebugger tricks I guess), we could not see any locals (“Internal debugger error”):

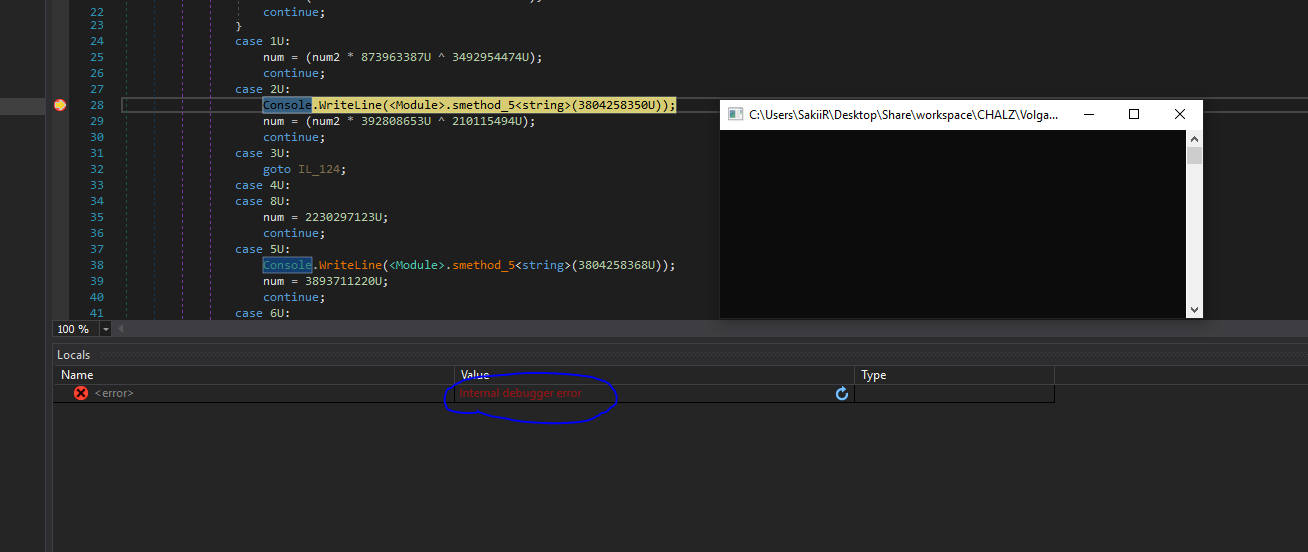
debugger_internal_error.png

You can see line 28 that the program is displaying some text on the screen. The function returning the string to display is highly obfuscated and might be hard to reverse. Here, the text returned is displayed to the screen, so we just need to step over to see which string is returned.

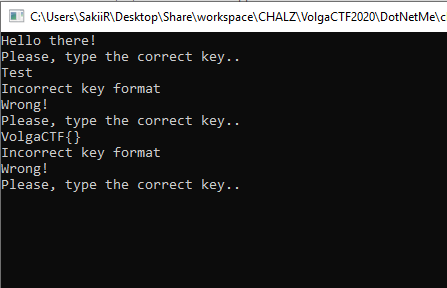
The Main() method of the first binary is just looping infinitely and wait for a “flag” to be sent:

cli.png

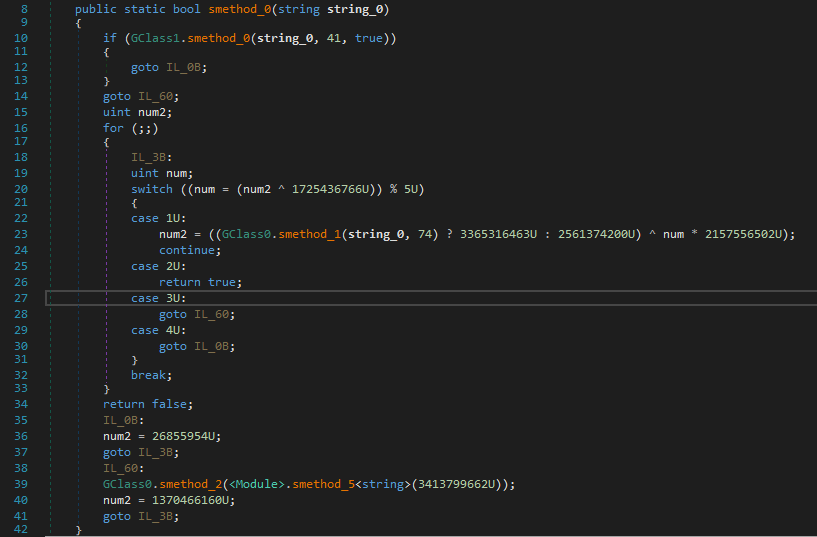
We can see that the interesting method called from main is located in the provided DLL:

check_flag.png

Since we can’t debug anything here, I decided to rewrite the code into Visual Studio so that we can debug the whole binary without any issue.

This way, a lot of variables and functions could be renamed and while debugging, all the scope variables can be read:

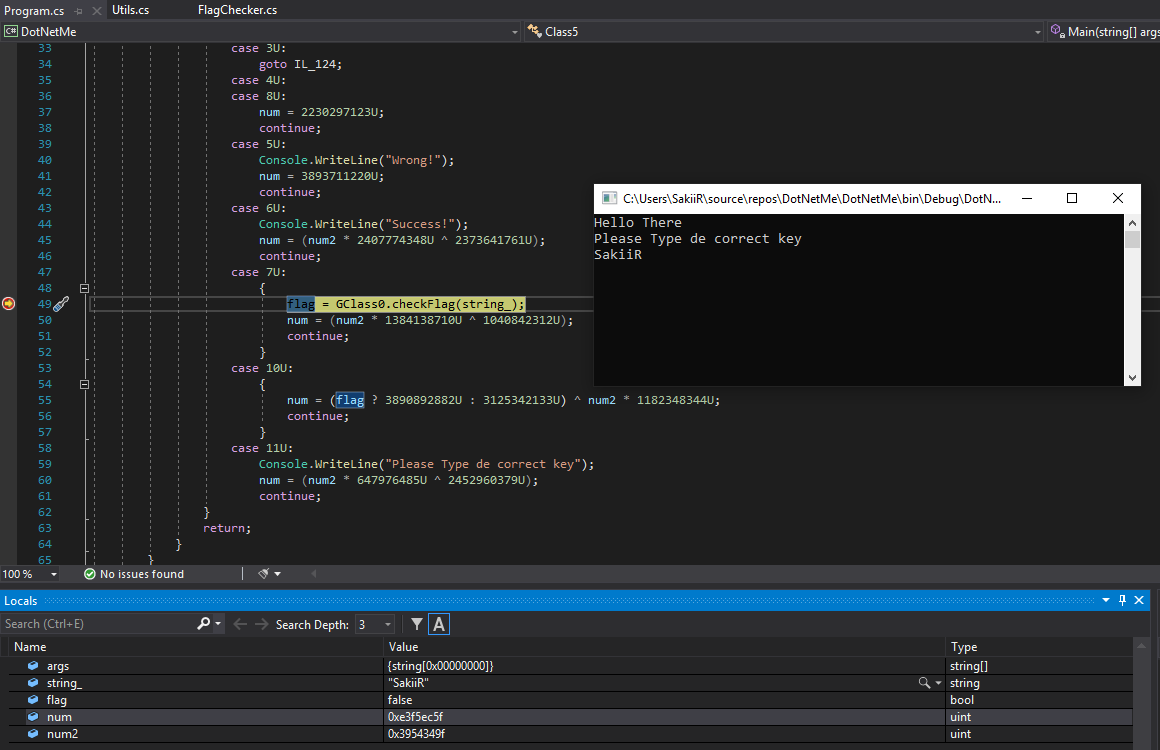
vs.png

I went further and saw that the key has to respect a specific format (num variable represent the state of the function - Branching condition):

Six ‘-’ separated blocks

num = (((GClass1.StringSplit(user_input, new char[]
{
'-'
}).Length == 6) ? 683502988U : 1473095498U) ^ num2 * 1113113859U);

Each block has to contain 4 characters

num = (GClass1.StringLength(input_parts[num3]) == 4) ? 161800768U : 267634710U;

The whole flag has to be 29 characters long

num = (((GClass1.StringLength(user_input) != 29) ? 650567720U : 925404683U) ^ num2 * 2388823709U);

Finally, all of these characters have to be between 0x20 and 0x7f

case 9U:
{
	num = ((c < '\u007f') ? 3945937441U : 3956362675U) ^ num2 * 3337894887U;
	continue;
}
case 10U:
{
	num = (((c < ' ') ? 2328726507U : 3166744977U) ^ num2 * 414064944U);
	continue;
}

From these conditions we can build a simple flag:

abcd-efgh-ijkl-mnop-qrst-uvwx

Another function is checking for “integrity”. In fact, this function that we called computeHash will hash all the characters and then check for the returned value to be equal to the second parameter:

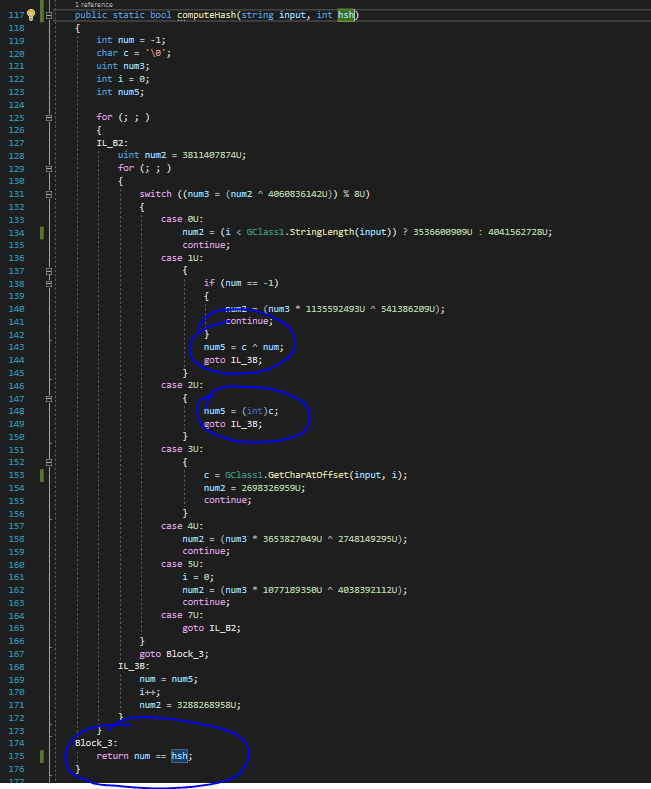
computeHash.png

We can build a simple python function from this C# code:

def computeHash(flag):
    i = 0
    ret = ord(flag[0])
    while i < len(flag) - 1:
        ret = ord(flag[i + 1]) ^ ret
        i += 1
    return ret

# computeHash('abcd-efgh-ijkl-mnop-qrst-uvwx')

In this case, the hash is computed and then compared to 41:

hash_check.png

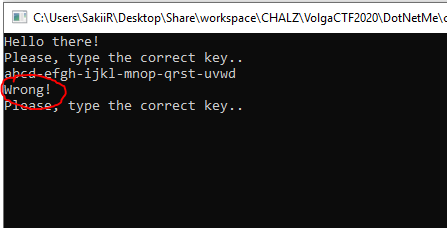
To match the first condition and go further we can simply replace the last ‘x’ with a ’d'. The message “Invalid flag format” will disappear:

no_invalid_format.png

Let’s go further, a last operation is performed on our user input with an unknown string. At the end of this function, a check is done on the flag (the same with computeHash), but this time, checked against ‘74’ and with the third parameter to false (this boolean make the function check or not check the input format: 0x20 > c < 0x7f, etc.).

In this capture, we can see that the string used “key” is still unknown (because of the heavily obfuscated function returning string from int):

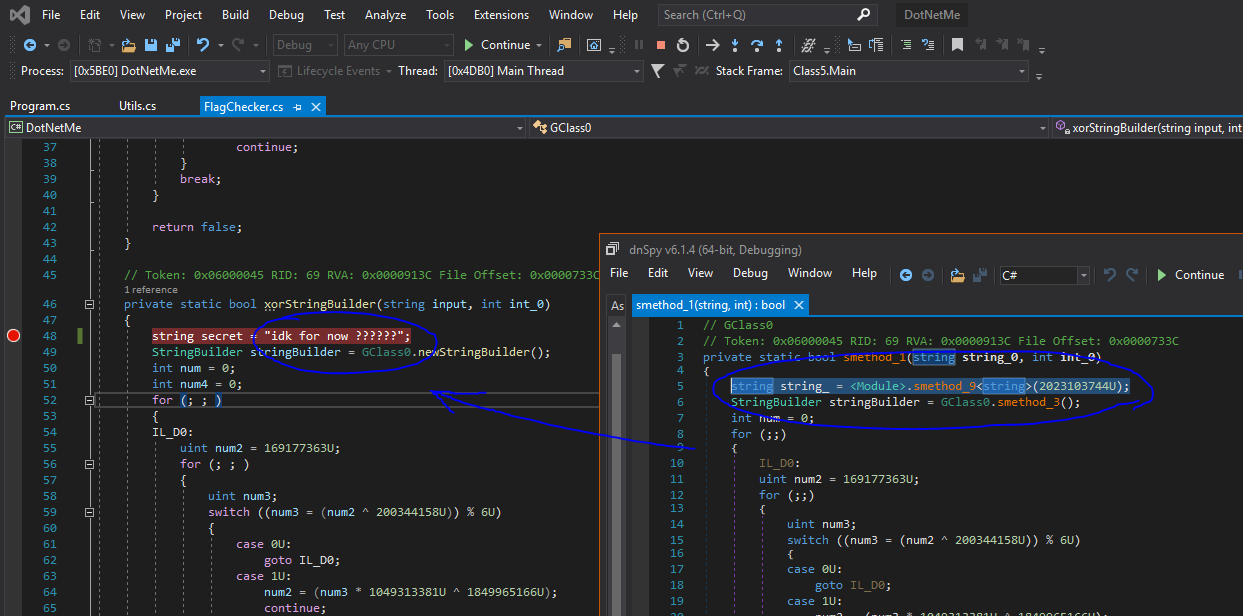
unknown_string.png

Earlier, we saw that string was retrieved through a “heavily obfuscated function.” Only one string remained unknown to me until I asked XeR to look into it. In fact, since the .NET standard library does not contain any antidebugger tricks, we could see all locals normally when going into it:

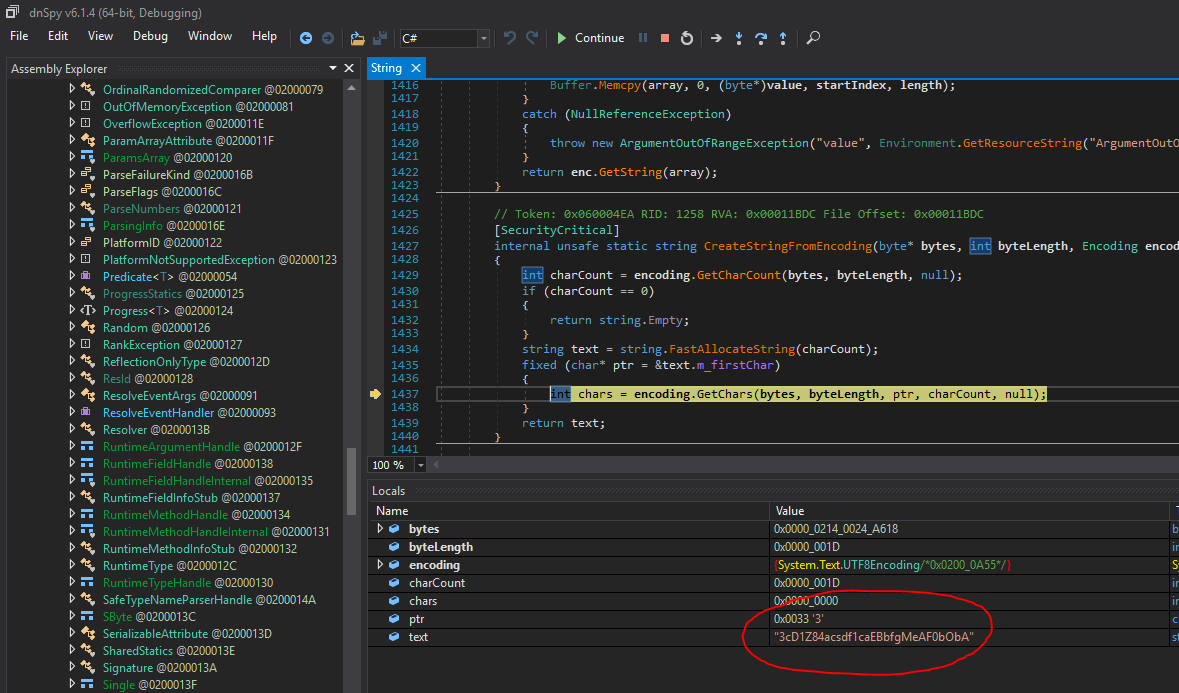
extracted_key.png

So we replaced the key, we go further with our special RE skills and write a python code from this cool function:

def last_step(flag):
    out = ""
    for i, c in enumerate(flag):
        num4 = ord("*") * ord(c)

        a = (num4 >> 5) + (num4 >> 4) & 127
        b = num4 + ord(c) & 127
        c = ord(flag[len(flag) - 1 - i])

        out += chr(a ^ b ^ b)
    return out

Here is the complete python script I made for the challenge “emulation”

#!/usr/bin/env python
# @SakiiR

import sys

KEY = "3cD1Z84acsdf1caEBbfgMeAF0bObA"
SUM1 = 41
SUM2 = 74


def computeHash(flag):
    i = 0
    ret = ord(flag[0])
    while i < len(flag) - 1:
        ret = ord(flag[i + 1]) ^ ret
        i += 1
    return ret


def checkFormat(flag, hsh):
    if len(flag) != 29:
        print(f"Bad format: bad length {len(flag)}")
        return False
    if len(flag.split("-")) != 6:
        print(f"Bad format: count split {len(flag.split('-'))}")
        return False
    for c in flag:
        if ord(c) < 20 or ord(c) > 0x7F:
            print(f"Bad format: Bad chr '{c}'")
            return False
    hsh_check = computeHash(flag) == hsh
    if not hsh_check:
        print(f"Bad format: Bad checksum '{computeHash(flag)}' != {hsh}")

    return hsh_check


def last_step(flag):
    out = ""
    for i, c in enumerate(flag):
        num4 = ord("*") * ord(c)

        a = (num4 >> 5) + (num4 >> 4) & 127
        b = num4 + ord(c) & 127
        c = ord(flag[len(flag) - 1 - i])

        out += chr(a ^ b ^ b)
    return out


def main(argv):
    if len(argv) < 2:
        print(f"USAGE: {argv[0]} FLAG")
        return

    flag = argv[1]
    if not checkFormat(flag, SUM1):
        print(f"Bad Flag {flag}")
        return False

    hsh = computeHash(last_step(flag))
    if hsh != SUM2:
        print(f"Bad Flag {flag}: Invalid hash '{hsh}' != {SUM2}")
        return False

    print(f"Flag {flag} Ok !")


if __name__ == "__main__":
    main(sys.argv)

Note that later, there will be a check on the output of this function. The output’s hash has to match the int “74”. This is not very convenient since this is the second hash computed for the same output. We are going to need some z3 skills to solve these constraints.

Hopefully, BitK helped with that and provided us a cool script generating a valid key:

from z3 import *


solver = Solver()

secret = b"3cD1Z84acsdf1caEBbfgMeAF0bObA"
key = [BitVec(f"input-{x}", 32) for x in range(29)]


def apply_format(arr):
    for c in arr:
        solver.add(c > 0x20)
        solver.add(c < 0x7F)

    for x in range(4, 29, 5):
        solver.add(arr[x] == ord("-"))


out = []
nums = []
for x in range(29):
    num4 = 42 * key[x]
    a = (LShR(num4, 6) + LShR(num4, 5)) & 127
    b = (num4 + secret[x]) & 127
    c = secret[28 - x]

    o = BitVec(f"out-{x}", 32)
    solver.add(o == (a ^ b ^ c))
    out.append(o)


def make_xor(arr):
    out = arr[0]
    for c in arr[1:]:
        out = out ^ c
    return out


solver.add(make_xor(key) == 41)
solver.add(make_xor(out) == 74)
apply_format(key)

if str(solver.check()) != "sat":
    exit(":(")

model = solver.model()

print("".join(chr(model[c].as_long()) for c in key))

The script outputs !sfc-glZa-6|/z-~pNd-p3oK-kTss which is valid against my script and the actual binary:

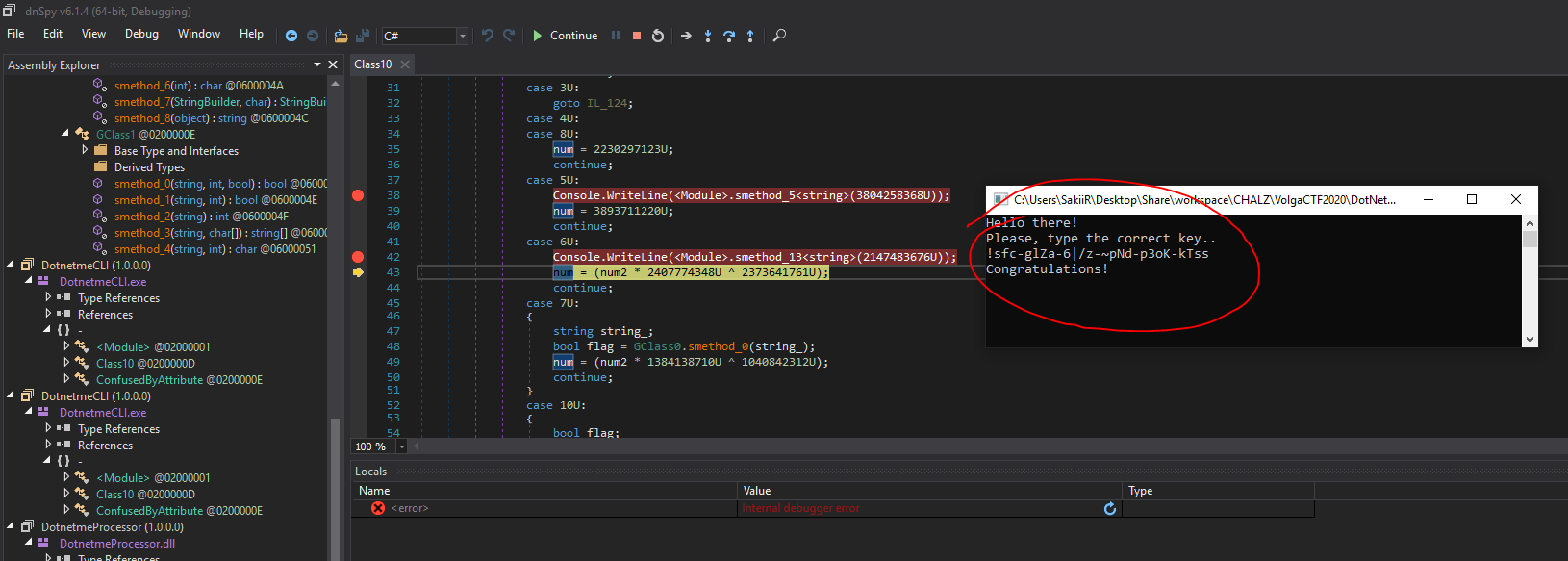
congratulation.png

Also work as a flag: VolgaCTF{!sfc-glZa-6|/z-~pNd-p3oK-kTss}

You can find my sources as an archive here: sources.

 - @SakiiR

 Thanks to @BitK and @XeR